Linked Lists

What is a Linked List

A Linked List is a sequence of Nodes that are connected/linked to each other. The most defining feature of a Linked List is that each Node references the next Node in the link.

There are two types of Linked List - Singly and Doubly. We will be implementing a Singly Linked List for this code challenge.

Terminology:

1. Linked List - A data structure that contains nodes that link/point to the next node in the list.
2. Singly - Singly refers to the number of references the node has. A singly linked list means that there is only one reference, and the reference points to the next node in a linked list.
3. Doubly - Doubly refers to there being two (double) references within the node. A doubly linked list means that there is a reference to both the next and previous node.
4. Node - Nodes are the individual items/links that live in a linked list. Each node contains the data for each link.
5. Next - Each node contains a property called next. This property contains the reference to the next node.
6. Previous - In a doubly linked list, each node contains a property called previous. This property contains the reference to the previous node.
7. Head - The head is a reference to the first node in a linked list.
8. Current - The current reference is a reference to the current node being looked at. The current reference is traditionally used when traversing through a full linked list, similar to how an index is used when traversing through an array.

What does it look like

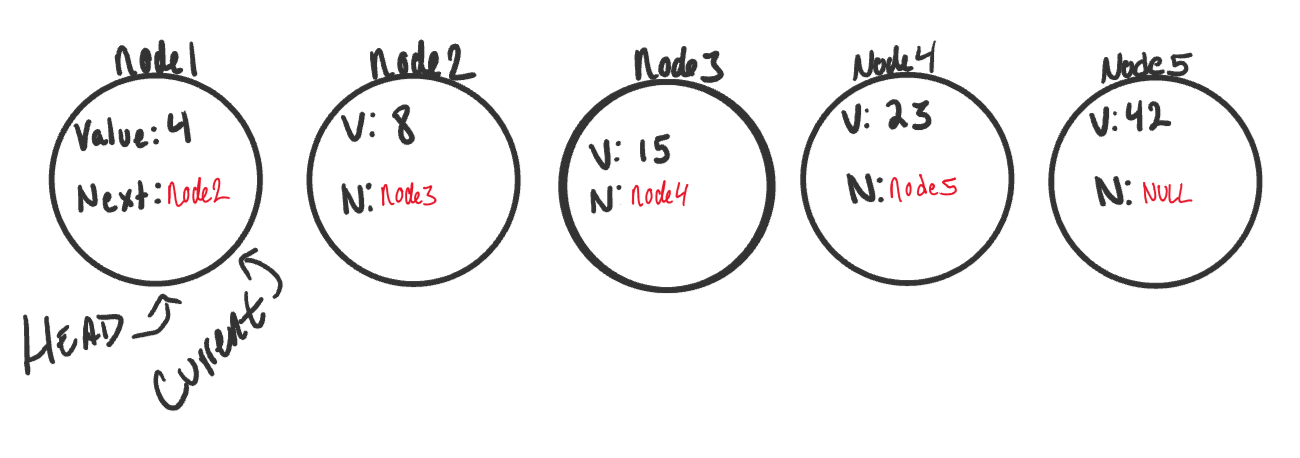
This is what a Singly Linked List looks like:

Traversal

When traversing a linked list, you are not able to use a foreach or for loop. We depend on the next value in each node to guide us where the next reference is pointing. The next value is exceptionally important because it will lead us where the next node is and allow us to extract the data appropriately.

The best way to approach a traversal is through the use of a while() loop. This allows us to continually check that the next node in the list is not null. If we accidentally end up trying to traverse on a node that is null, a NullReferenceException gets thrown and our program will crash/end, so we usually need to have some check in our loop for that case.

When traversing through a linked list, the current node is the most helpful. The current will tell us where exactly in the linked list we are and will allow us to move/traverse forward until we hit the end.

Example

Let’s put a use case on our traversal. We want to check whether or not our LinkedList includes a specific value.

The pseudo-code for an includes is as so:

ALGORTIHM includes (value)
// INPUT <-- integer value
// OUTPUT <-- boolean

	current <-- head

	WHILE current is not NULL
		IF current.value is equal to value
			return TRUE

		current <-- current.next

	return FALSE

Let’s talk out what exactly is happening:

1. We are first setting current to the head to guarantee we are starting from the beginning. (Remember that head is always the first node in a Linked List)

2. We create a while loop. This loop will only run if the node that current is pointing to is not null. This also means we can guarantee that we are still looking at a node while the loop is running.

3. Once we are in the while loop, we are checking if the value of the current node is equal to the value we are looking for. Given the logic, if that condition is true, then we have found the value we were looking for, so we return true.

4. If the current node does not contain the value we are looking for, we then must move current to the next node that is being referenced. Again, because the condition of this while loop is to only run if we are still at a node, we can safely traverse to the next node without fear of getting a NullReferenceException.

5. At this point, the while loop is re-evaluated. Step 3 & 4 will continue until current reaches the end of the linked list. We will know we are at the last node in the linked list because the current node will be null. Once this condition becomes true, the while loop breaks, and we now know that we are at the end.

6. Once we hit the end, we know that we did not find the value and return true at any point, so the value is not in the linked list. We return false.

Big O

The Big O of time for includes would be O(n). This is because, at its worse case, the node we are looking for will be the very last node in the linked list. The variable n represents the number of nodes in the linked list.

The Big O of space for includes would be O(1). This is because there is no additional space being used than what is already given to us with the linked list input.

Adding a Node

Adding O(1)

Order of operations is extremely important when it comes to working with a linked list. What I mean by this is you must be careful that all references to each link/node is properly assigned.

An example can be with adding a node to a linked list. If we want to add a node with an O(1) efficiency, we have to replace the current head of the linked list with the new node, without losing the reference to the next node in the list.

Here are the required steps to add a new node with an O(1) efficiency.

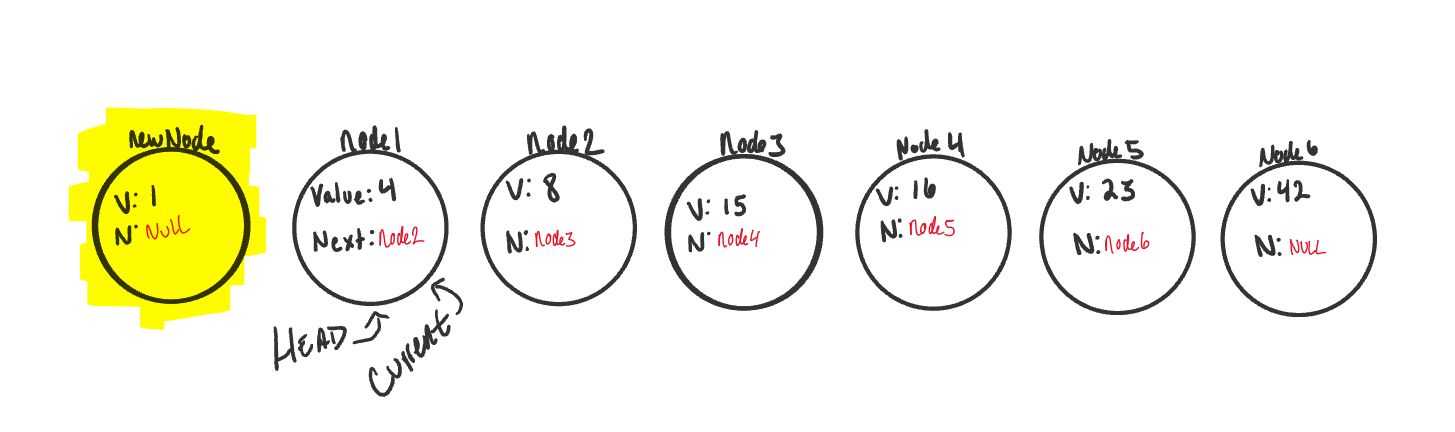
1. Set current equal to head. This will guarantee us that we are starting from the very beginning.
2. We can then instantiate the new node that we are adding. The values passed in as arguments into the add() method will define what the value of the Node will be.

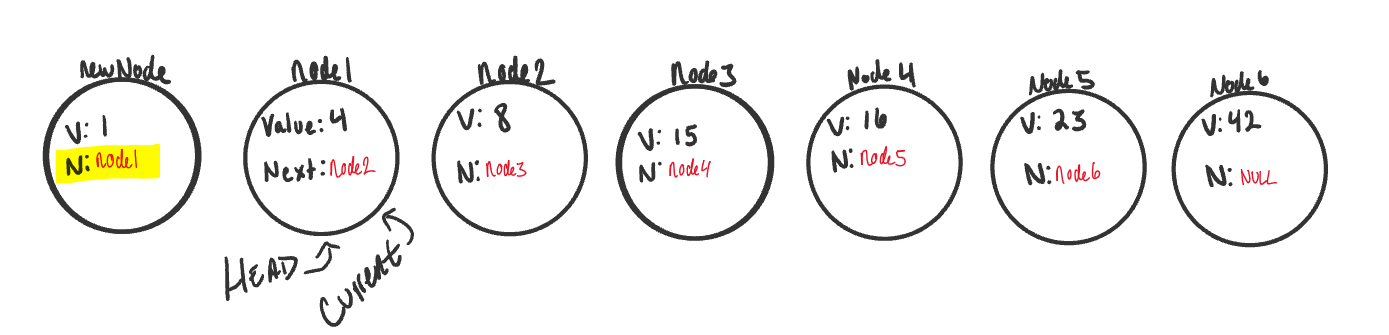
1. newNode.next by default is set to null. We want to set newNode.next property to the same location that the head node is pointing towards. Because head is just a reference type, we will be assigning it to the same allocation in memory as the node it is pointing too. In this case, it’s Node1.

1. At this point in the program we now “technically” have newNode at the beginning of the linked list, but we are not done yet. We now have to re-assign where head is pointing too. Since Node1 is no longer the first node in the list, we want to re-assign head to point at newNode.

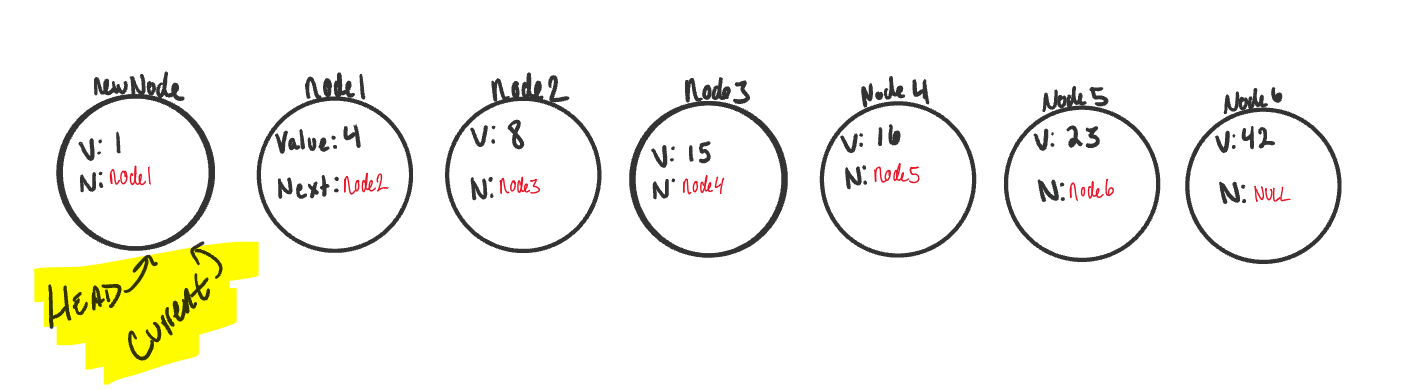
2. While we are at it, let’s just re-assign current as well to make sure that any further operation starts at the new true start of the linked list.

Code

Here is the Pseudo code for an add method on a Linked list

ALGORITHM add(newNode)
// INPUT <-- Node to add
// OUTPUT<-- No output

	current <-- head
	newNode.next <-- head
	head <-- newNode
	current <-- head

Big O

Regardless of the number of nodes that this linked list has, it will always be a O(1) time and space because it takes the same amount of time to add a new node to the beginning of the list, and no additional resources are being used.

Adding a Node O(n)

Adding a node to the middle of a linked list is a bit different than adding to the beginning. This is because we are working with more nodes and must re-allocate to make room for the new node.

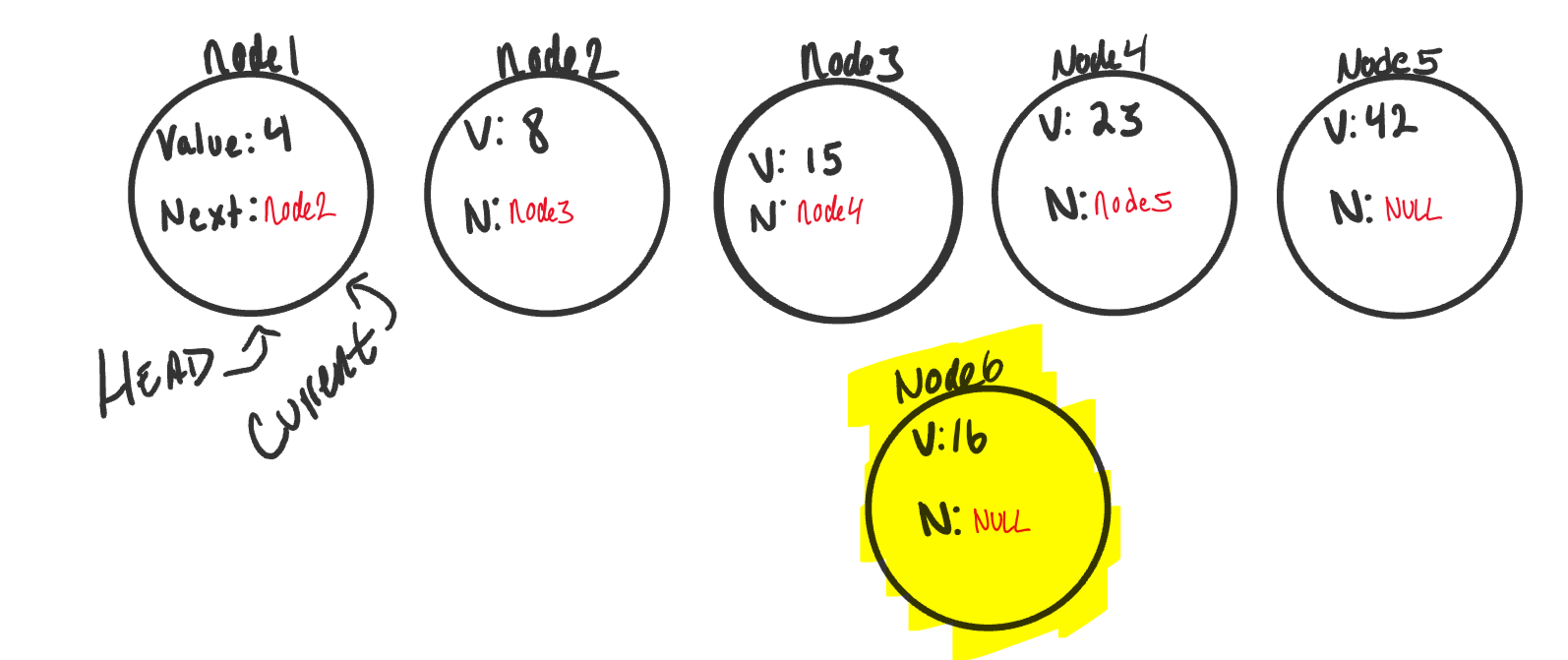
1. Let’s start out with a basic Singly Linked List:

1. Now let’s create a new node (node6). We will set the value of node6 to be 16. The next will be null because we haven’t yet attached it into the linked list.

1. Now let’s start the adding. We can do an addBefore method or an addAfter. For this documentation, we will do an addBefore. The addAfter is extremely similar…see if you can figure it out on your own!

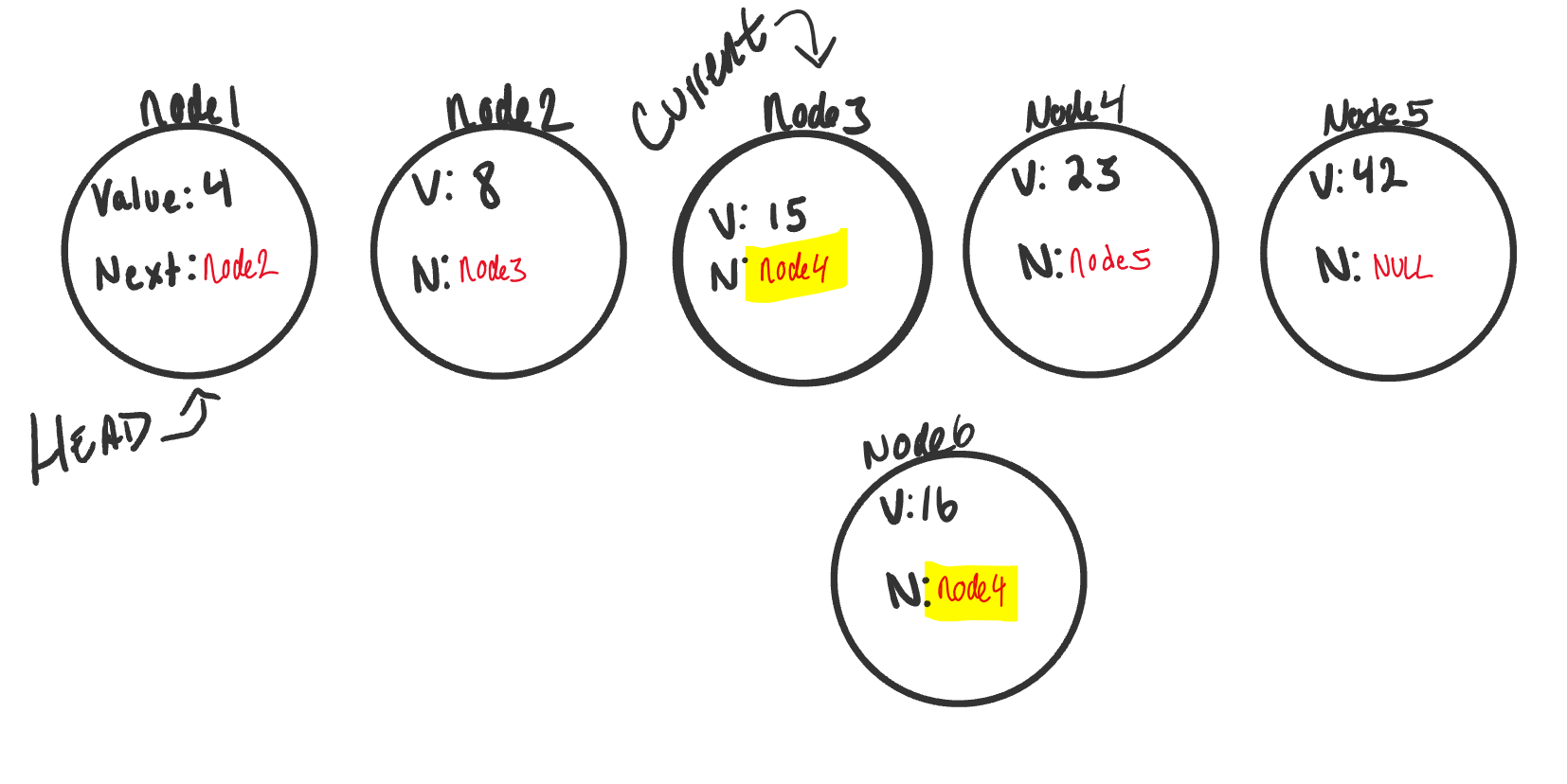
Our addBefore method will insert node6 before node4.

We already learned how to traverse earlier, and that is exactly what we want to do now. We will traverse while the next node is not null. Before moving current to the next node, we want check if the value of the next node is equal to the value we are supposed to be watching for (the value of the existing node we are inserting before). If it is, we want to set the new node (node6)’s .next equal to the existing node.

The linked list image above is in the following state:

1. current is pointing to node3.
2. node3.next property is equal to node4.
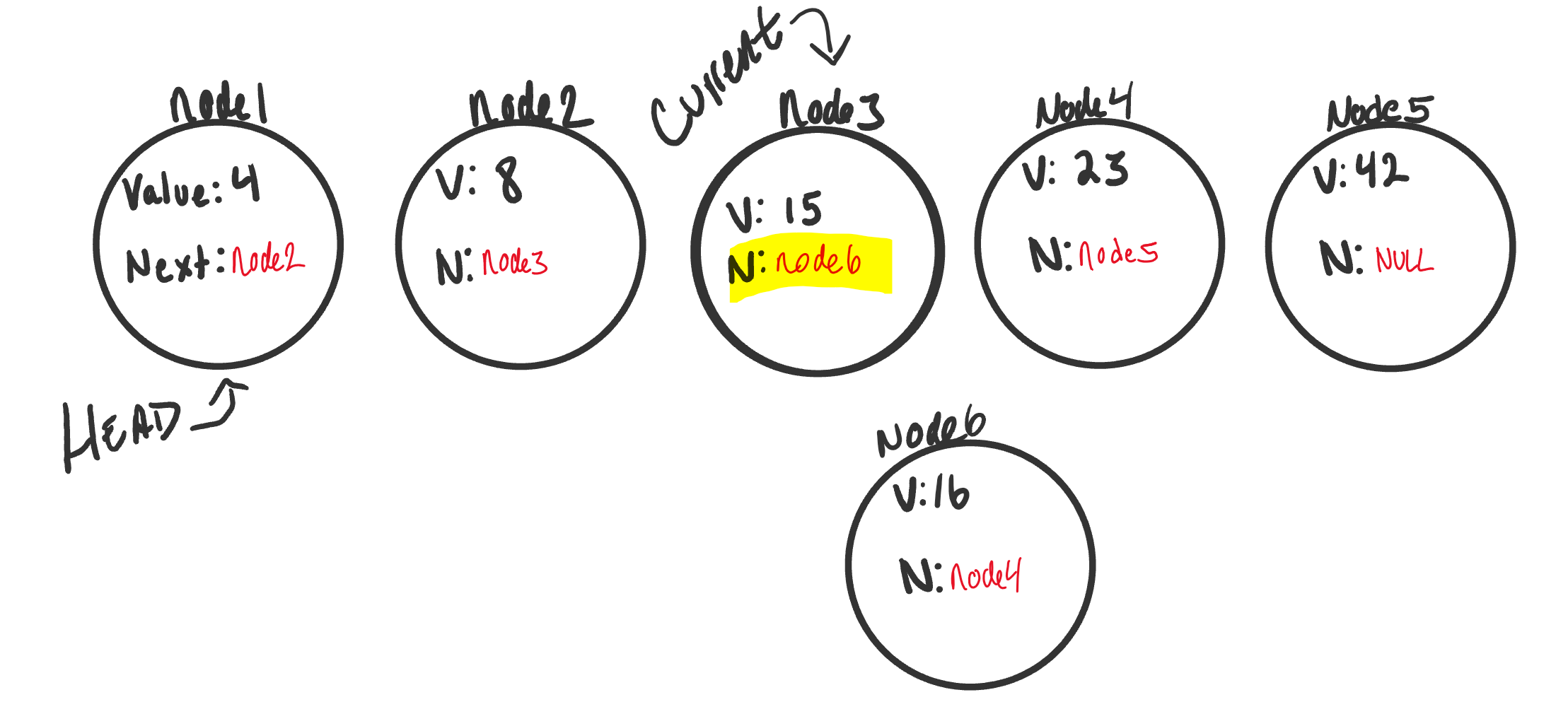
3. Since this is the node we want to insert before, we can now set our node6.next property also to node4. We do this at the time the node is found to prevent setting node6.next to a node that may not exist.
4. Uh-Oh, now both node3 and node6 are pointing to the same next node. node6 is not quite fully apart of the linked list.
5. Next, we have to adjust node3.next to point to the newly created node, node6. Since we still have current pointing to node3 this will be a straightforward transaction. We just simply tell current (because it is pointing to the same memory location as node3) to change it’s next to point to the new node (node6).

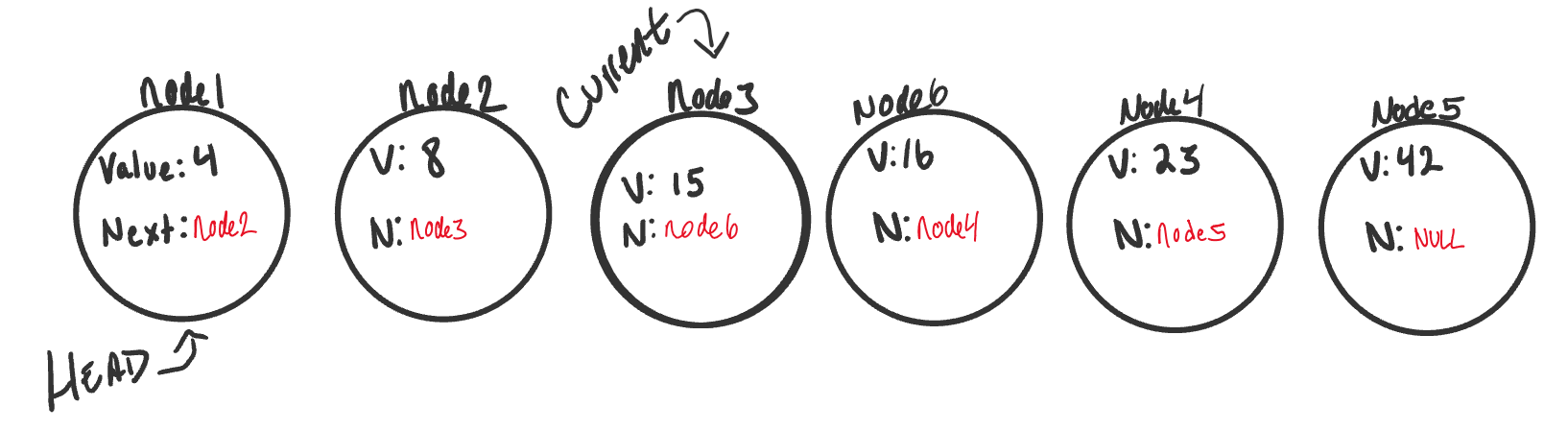
And now we have a complete linked list with the newly added node exactly where we wanted it.

Code

Here is the Pseudo code for an addBefore method in a linked list

ALGORITHM addBefore(newNode, existingNode)
// INPUT <-- New Node, Existing Node
// OUTPUT <-- No Output

	current <-- head

	while current.next is not equal to NULL
		if current.next.value is equal to existingNode.value
			newNode.next <-- existingNode
			current.next <-- newNode

		current <-- current.next;

Big O

The time efficiency of this transaction would be O(n) because we could be inserting the new node, worst case scenario, at the end. With n being the number of nodes possible, we would therefore have O(n) time efficiency.

Space efficiency would stay at an O(1) because, like before, no additional space is being used allocated outside of what is given to us on the input.

Print Out Nodes

Printing out all of the nodes in a Linked List is very similar to what we did in the find() method. This is because we are leveraging our current node and a while loop to traverse through the existing linked list.

Here is the pseudo code for a method to print out all the nodes in a linked list:

ALGORITHM print()
// INPUT <-- None
// OUTPUT <-- string to console

	current <-- head

	while current.next is not equal to NULL
		OUTPUT <-- "current.value --> "
		current <-- current.next

	OUTPUT <-- "current.value --> NULL"

Much like in the find, we are creating a while loop to check and make sure we are not at the end of a linked list. Right before the while loop restarts, we move current to the next node in the list.

Once we hit the end, we write out the last node, and then show that it is pointing to null.

Prerequisites

When constructing your code, a few things to keep in mind.

1. When making your Node class, consider requiring a value to be passed in so that each node has a value.

2. When making a linked list, you may want to require that at least one node gets passed in upon instantiation. This first node is what your head and current will point too.