K-Nearest Neighbors Classifier¶
Another classifier, the K-Nearest Neighbors algorithm seeks to categorize new data based on the labels of the K closest data points. “Closeness” is determined by the distance between test point \(p\) with characteristics \((p_1, p_2,..., p_N)\) and another point \(q\) with characteristics \((q_1, q_2,..., q_N)\).
The distance between any two points can be calculated as
\[d = \sqrt{(p_1 - q_1)^2 + (p_2 - q_2)^2 + ... (p_N - q_N)^2}\]
Assuming that \(p\) and \(q\) are NumPy arrays, the function for measuring distance is:
import numpy as np
def distance(p, q):
return np.sqrt(np.sum((p - q)**2))
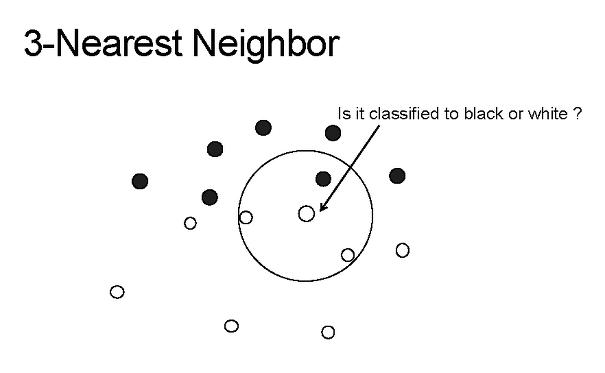

The Algorithm¶
- Use characteristics of interest to calculate the distances between point \(p\) and all other points
- Sort points in order of distance from \(p\)
- Keep the first \(K\) points
- Tally the number of points in each class
- If the tally is tied between classes, reduce K by 1 and count again
- Assign to \(p\) the class with the highest total
Advantages¶
- The cost of the learning process is zero
- Often successful when labeled data is well-mixed or data boundaries are irregular.
Disadvantages¶
- Very inefficient for large data sets
- There’s no real model to interpret
- Performance depends on the number of dimensions
- Inconsistent results when there’s ties in votes
Attributes¶
- neighbors: the number of nearby points from which to inherit a label
Operations¶
- clf.predict(full_data, test_data): given some full data set, predict the classifications on a new data set of one or many points.
