Binary Search Tree¶
Definition¶
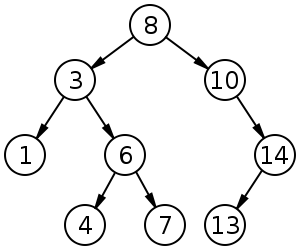
A binary search tree is a data structure that allows for fast lookup (log N), addition, and removal of items. Every item in a binary search tree (hereon called a “Node”) is related to every other item by its key.
If the tree is empty, then a new node inserted into the tree becomes the tree’s root. The next node inserted will have its key compared to the key of the root node. If lower, it will occupy the “left” attribute of the root node. If higher, it occupies the “right” attribute. If a node tries to occupy the “left” or “right” attribute of the root and that attribute is already occupied, it moves down the tree to that node and has its key compared again.
On average, each comparison allows searching to ignore half of the tree. As such, each search takes time proportional to the logarithm of the number of items stored in the tree.
Attributes¶
Node¶
- key - the identifier of the node.
- value - the data each node holds. A simple tree may only have nodes whose values are the keys.
- left - the next node whose key is less than the current one. Can be null.
- right - the next node whose key is greater than the current one. Can be null.
Tree¶
- root - a pointer to the first node in the tree
- size - the number of nodes in the tree; example above has size 9
- depth - the lowest level to which the tree extends; example above has depth of 3
- balance - an integer representing how well-balanced the tree is. Trees which are higher on the left than the right are positive; trees which are higher on the right than the left are negative. A balanced tree has a balance of zero.
Operations¶
insert()- adds a new node to the treecontains()- returns whether or not the tree contains the given node
